Criterio de Stolz del cociente
Normalmente, para calcular límites de sucesiones utilizamos los razonamientos que aplicamos a las funciones. Sin embargo, cuando esto no es posible, recurrimos a criterios específicos para sucesiones. Uno de ellos es el criterio de convergencia de Stolz del cociente.
Criterio de Stolz del cociente
Sean y dos sucesiones, siendo estrictamente monótona y cumpliéndose una de las dos siguientes condiciones:
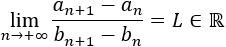 Entonces,
Entonces,
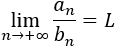 Nota 1: el límite L debe ser finito.
Nota 2: en algunos casos particulares, puede ayudar escribir el primer límite del teorema como
Nota 1: el límite L debe ser finito.
Nota 2: en algunos casos particulares, puede ayudar escribir el primer límite del teorema como
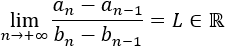
- →0, →0 y es decreciente.
- →+∞ y es creciente.
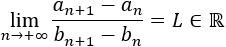 Entonces,
Entonces,
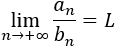 Nota 1: el límite L debe ser finito.
Nota 2: en algunos casos particulares, puede ayudar escribir el primer límite del teorema como
Nota 1: el límite L debe ser finito.
Nota 2: en algunos casos particulares, puede ayudar escribir el primer límite del teorema como
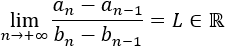
Ejemplo
Calculamos el límite de la sucesión
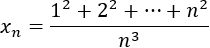 La sucesión del denominador es estrictamente monótona creciente y divergente.
Vamos a operar un poco para calcular el límite del cociente del criterio de Stolz:
El numerador de dicho cociente es
La sucesión del denominador es estrictamente monótona creciente y divergente.
Vamos a operar un poco para calcular el límite del cociente del criterio de Stolz:
El numerador de dicho cociente es
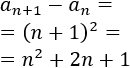 El denominador es
El denominador es
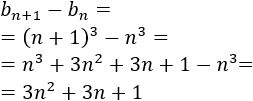 Calculamos el límite:
Calculamos el límite:
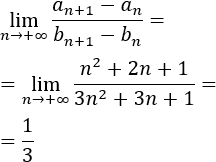 Como el límite es finito, por el criterio de Stolz, la sucesión es convergente a 1/3.
Más ejemplos: Criterio de Stolz del cociente: enunciado y ejemplos.
Como el límite es finito, por el criterio de Stolz, la sucesión es convergente a 1/3.
Más ejemplos: Criterio de Stolz del cociente: enunciado y ejemplos.
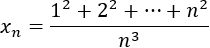 La sucesión del denominador es estrictamente monótona creciente y divergente.
Vamos a operar un poco para calcular el límite del cociente del criterio de Stolz:
El numerador de dicho cociente es
La sucesión del denominador es estrictamente monótona creciente y divergente.
Vamos a operar un poco para calcular el límite del cociente del criterio de Stolz:
El numerador de dicho cociente es
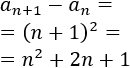 El denominador es
El denominador es
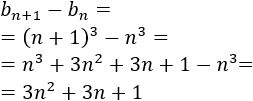 Calculamos el límite:
Calculamos el límite:
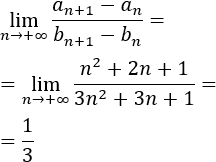 Como el límite es finito, por el criterio de Stolz, la sucesión es convergente a 1/3.
Más ejemplos: Criterio de Stolz del cociente: enunciado y ejemplos.
Como el límite es finito, por el criterio de Stolz, la sucesión es convergente a 1/3.
Más ejemplos: Criterio de Stolz del cociente: enunciado y ejemplos.Recursos
Criterios de convergencia:
- Criterio de la media aritmética
- Criterios de la media geométrica y de la raíz
- Criterio de Stolz del cociente
- Test básico
- Tipos de sucesiones
- Progresiones aritméticas
- Progresiones geométricas
- Problemas de progresiones aritméticas y geométricas
- Sucesión de Fibonacci
- Calculadoras de progresiones aritméticas
- Calculadoras de progresiones geométricas
- Operaciones entre sucesiones
- Límites de sucesiones
- Subsucesiones
- Introducción a las sucesiones (PyE)