Definition des Monotoniebegriffs
Eine Funktion ist in einem Bereich streng monoton wachsend, wenn dort ihre Ableitung stets positiv ist.
Sie ist in einem Bereich streng monoton fallend, wenn dort ihre Ableitung stets negativ ist.
Das "streng" bedeutet, dass es wirklich bergauf/bergab gehen muss, dass also die Ableitung nicht Null werden darf. Wenn man von monoton wachsend/fallend (ohne streng) spricht, darf die Ableitung auch Null sein.
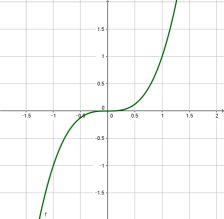
Beispiel 1
Die Funktion ist auf dem offenen Intervall () streng monoton steigend. Auf dem halb-offenen Intervall (] ist sie jedoch nur monoton steigend. Ebenso auf ganz , denn in beiden Fällen ist die Stelle mit der Ableitung im Bereich enthalten.
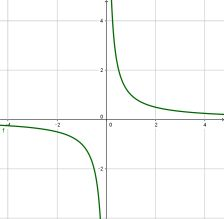
Beispiel 2
Die Funktion ist auf und auf streng monoton fallend und damit auf ihrem gesamten Definitionsbereich. (Bei der "Problemstelle" x=0 ist die Funktion ja gar nicht definiert)