Наочності і завдання до теми: "Геометричні перетворення на площині "
Поняття симетрії відносно точки
Перетворення фігур за допомогою переміщення має декілька видів. Сьогодні ми ознайомимося з перетворенням фігури за допомогою симетрії відносно точки.
Точки X і X1 називаються симетричними відносно точки О, якщо точка О є серединою відрізка ХХ1 (рис. 160).
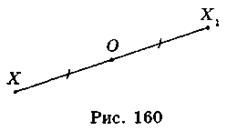
Центр симетрії
Точка О називається центром симетрії. Перетворення фігури F на фігуру Ft, при якому кожна точка X фігури F переходить у точку Х1 фігури F1, симетричну точці Xвідносно даної точки О, називається перетворенням симетрії відносно точки О. ФігуриF і F1 називаються центральносиметричними (симетричними відносно точки О) (рис. 161).
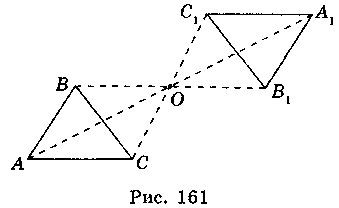
Властивості симетрії відносно точки (центральної симетрії)
- 1) Перетворення симетрії відносно точки є переміщенням.
- 2) Перетворення симетрії відносно точки перетворює пряму на паралельну їй пряму або на себе; відрізок — на рівний і паралельний йому відрізок; многокутник — на рівний йому многокутник.
- 3) Будь-яка пряма, що проходить через центр симетрії, відображається при цій симетрії на себе. Якщо перетворення симетрії відносно точки О переводить фігуруF (рис. 162) у себе, то вона називається центральносиметричною, а точка О — центром симетрії.
Питання 1.
Які перетворення називаються симетрією відносно даної точки?
Питання 2.
Як називаються фігури утворені подібним перетворенням*